If you are a math teacher, you teach or use the distributive property at least once during the year but sometimes more. Today while reviewing the properties of exponents, I realized I could apply the idea of distribution to one of the exponent rules.
If its in algebra we have something like 3(X + 2) or if its elementary we might use 10(3 + 2). We multiply the outside number or varible with each term inside the parenthesis. Pretty standard stuff except about 1/3rd of the students forget the second term so the first might end up as 3x + 2 instead of 3x + 6. As for the other, if you have students who remember PEMDAS, they are likely to ask why we don't add 3 + 2 first since that is what you are supposed to do. That is a discussion for another day.
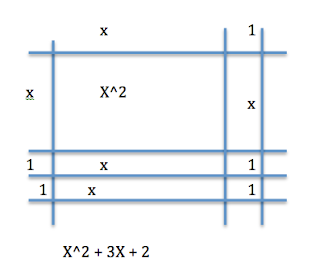
I also use the distributive method as one of the ways I teach multiplication of binomials.
I have students split the first binomial so the 2x is on the left and 3 is on the right. I keep the second binomial whole place one by the 2x and the again by the 3 as in the photo to the right.
Multiply, then combine common terms and you have an answer.
I've found several of my students actually prefer this method to the foil because they find it less confusing.
Today I reviewed the rules for exponents. You know the ones we all know by heart. If you are multiplying terms with exponents and they have the same base you add exponents.
X^2 * x^3 * x^2 = x^7
The one my students have trouble is the power to a power where you multiply exponents. They get it if there is one variable such as (x^2)^5, they know to multiply the exponents and get x^10. They run into problems if its a bit more extensive such as (2x^2y^5)^5
I realized today the processes is similar to the distributive property because you are multiplying the exponents of the terms inside the parenthesis by the exponent outside.
If you see the drawing, I've removed the terms and only looked at the exponents to show my students how you multiply each one.
We are distributing the outside across the inside so why can't we include this property to reinforce the process? I did see a few light bulbs go off in the crowd because they could relate the process to prior knowledge.
I am always looking for ways to activate prior knowledge and this seemed like a good way to do it.
I would love feedback on how you all see this as a way to teach this topic? Do you think its good or am I way off base? Thanks for your comments ahead of time.
Wednesday, August 31, 2016
Tuesday, August 30, 2016
Math Dude
 I was looking around for a nice video on solving one-step equations but was having trouble until I found a series of videos by Math Dude. Math Dude is also known as Mike Degraba who prepared a series of math videos for the Montgomery Public Schools in Maryland.
I was looking around for a nice video on solving one-step equations but was having trouble until I found a series of videos by Math Dude. Math Dude is also known as Mike Degraba who prepared a series of math videos for the Montgomery Public Schools in Maryland.The video lasted about 9:30 seconds and it kept students enthralled until the end. It had wonderful explanations, illustrations and was crazy enough to make the kids like it.
There are 31 different videos covering topics from graphic representations to solving equations, to finding slope and the equation of a line, to solving systems of equations to solving equations by factoring and so much more.
What impresses me most besides the fact you can down load the videos for free from the website, and the creations are extremely professional in appearance. The volume is great so no one is straining to hear the material. The inserts are easily seen and the Math Dude uses two cameras and looks directly at one or the other.
The video on solving one step equations began outside with the Math Dude and several children balanced on a see-saw. When two students got off, it showed balance but when one got off, Math Dude fell off because it was no longer balanced.
As he instructs, an inset shows the math as he speaks so students see what is going on. He used word problems to show the translations from words to math and then showed how to solve problems using each of the four operations. Its very clear. I liked that each operation was shown separately so students could see the process.
Most of the videos range in length from 6 to 13 minutes. Each video is filled with humor, instruction, and information on so much more. His sense of humor shines through and captivated each and everyone of my students.
Check him out, if not at the school website, he can be found on Youtube. Just type in Math Dude and the videos will pop up.
Monday, August 29, 2016
Elaboration in Math
 Elaboration in the English means you go into great detail on something. It might be adding lots of detail to something but does it apply in the same way to Math? Lets look first at what elaboration is as a learning technique.
Elaboration in the English means you go into great detail on something. It might be adding lots of detail to something but does it apply in the same way to Math? Lets look first at what elaboration is as a learning technique.Elaboration is a conscious way of expanding a topic or idea so a student can process it more thoroughly. One method of elaboration is to take information and turn it into a question.
You might read that warm air rises so you might ask "Why does warm air rise?" Finding the answer to this question leads you to think about why it might be lighter than colder air.
The materials you know well are called anchor points because it is easy to recall. The more anchor points you have, in place, the the more meaningful the information becomes and the easier it becomes to remember it. It helps in the process of learning. So elaboration helps form a bridge between the new information and previous knowledge.
This leads us to ask how would we turn the information into questions in Math. Today I taught x^0 = 1. Is it possible to ask "Why does x^0 = 1" Yes because of the rules of division of exponents. X^3/X^3 = 1 becomes X^3-3 = 1 which gives us X^0 = 1.
What about other topics such as solving one step equations. One of the standard ways of teaching this topic is to talk about undoing or doing the opposite to solve it. Can we ask "Why do we do the opposite operation to solve the equation?" I think we can but the question asked needs to lead to real thought. For instance when you teach binomial multiplication, you could be asking a couple of different questions to help elaborate the material.
First you might ask "Why do we need to multiply binomials" followed by "Why do we end up with three terms?" Both of these questions make you acquire a deeper knowledge. However, research shows that students learn better if they generate the associations rather than having them provided. So its important for the students to learn to create their own questions rather than relying on the ones the teacher provides.
Suggestions to help students learn methods of elaboration include:
1. Gaining attention by asking them how the material is relevant to them. This might be seeing how the math is used in real life, or how they might use it in the future. Most students I know will fall back on the "I need to know it for the test!"
2. Simulation recall when you ask them to recall something that is similar to the new material. When looking at binomial multiplication, they might comment that the method you are teaching is similar to the way they learned to multiply regular numbers in elementary school.
3. Present the material by presenting examples and asking them to find the common concept among the examples. It is possible to ask students how this new concept compares with a previous concept. One possibility here is using the distributive method for binomial multiplication and asking students to compare it with the distribution property.
4. Error correction where a student explains why the problem was wrong and what is the correct way of doing it. I ask students to do this for all questions they missed.
Give this some thought and see how this might be used in your classroom.
Sunday, August 28, 2016
Saturday, August 27, 2016
Friday, August 26, 2016
Cool Arguments
 This has been a very interesting week in my math classes. I've had a couple students who came up with interesting points in two different math classes.
This has been a very interesting week in my math classes. I've had a couple students who came up with interesting points in two different math classes.This week, I've spent time helping the geometry class do some basic vocabulary work using the Freyer model which requires a definition, fact, example and non-example for each work.
I started them with point, ray, line, line segment, midpoint and intersection. So of course when the non-example came up, the kids thought they would be silly and called out apple or pine cone which I said were great. When we got to intersection, one child called out "A mountain!" for a non-example of an intersection. Another child disagreed.
Her argument was beautiful. She said it did represent an intersection because it was the bottom part of the intersection and the top of the mountain was at the actual point of intersection. This is out of a 9th grader. This lead to a really interesting discussion and the final conclusion from the class boiled down to the two lines did not extend all the way after crossing so it was a non-example. After all, an intersection of roads continued after they crossed. I let them draw their own conclusion on this argument.
The other interesting conclusion came from the Algebra I class with their review of exponents. I asked for examples of exponents in real life and most students came up with scientific notation but one student provided a variation.
He pointed out that we use exponents when we label the answer to area or volume problems. A couple students disagreed because the number itself did not repeat but the student stated the unit was being repeated.
To finish of this exponent question of can units be repeated, I'm having students create a piece of art where they choose an item like a piece of candy, draw it with an exponent and state that is equal to the item times itself.
For instance, a ice cream cone squared equals a ice cream cone times an ice cream cone. I hope this reinforces the basic concept of exponents. Let me know what you think of my student's arguments.
Thursday, August 25, 2016
Dual Coding in Mathmatics
 Another learning strategy is dual coding which is simply a way of writing and visualizing the material. It is combining text with pictures because it is believed that the brain remembers the information better when using both.
Another learning strategy is dual coding which is simply a way of writing and visualizing the material. It is combining text with pictures because it is believed that the brain remembers the information better when using both.Dual coding refers to two distinct types of coding. Analog coding which refers to the what the brain uses to process images while symbolic coding is where the brain processes writing as a mental representation of text. In symbolic coding the brain knows the letter x in certain contexts represents a variable.
In addition, there are three types of processing associated with dual coding. First is representational which directly triggers visual or verbal recognition. The second is referential where the verbal triggers the non-verbal or vice versa. Finally is association which where verbal triggers verbal and non-verbal triggers non-verbal.
Did you know there is more research supporting dual coding than there is for learning styles? The idea behind dual coding is that using both pictorial and writing are associated with higher levels of informational recall.
Did you know that until we can name a concept or explain how it is associated with other ideas, our brains have difficulty remembering it or even applying it. Part of this is that our brain has dual processing where pictures are processed on the right side while written is processed on the left side. In other words both sides of the brain share the load for learning the material.
So where does this leave us in math? All it means is that we need to provide students with both verbal and non-verbal representations through the use of manipulatives, pictures, etc. This is important for students to learn the material. Years ago, I had a high school student who learned for the first time that when drawing pictures for fractions such as 2/3, the 3 divisions had to be of equal size. She thought you could use any three divisions and it was fine.
I've used other representations that students have used. I just realized that for all the ways I teach binomial multiplication, they all boil down to :
This is the visual I use to for binomial multiplication. I have students who use this to multiply while others choose a different method.
So try to use both visuals and text in your lectures to help students learn the material better.
Wednesday, August 24, 2016
Spaced Retrieval in Math
 Spaced retrieval and retrieval practice are proving their worth in helping students learn and retain math. Research shows that testing done in the proper manner helps improve learning but that is the key.
Spaced retrieval and retrieval practice are proving their worth in helping students learn and retain math. Research shows that testing done in the proper manner helps improve learning but that is the key.Most of us think or testing as a form of assessment or as a way for the state to determine the effectiveness of the school but it doesn't have to be that way.
What spaced retrieval and retrieval practice boil down to is simply giving students a way to frequently practice retrieving the material. So how would that look in math?
One form might be using the smart board to present the question while students work out the answer and vote for the correct one using a clicker. It might be having the students work out the problems on their iPads and hold up the finished product so you have a quick glance.
Since I have not gotten my iPads yet this year, I had each individual person do the problem, check with their table mates to make sure they all had the same answer before sharing it with me. This worked quite well with these students.
According to Scientific American taking the test and providing well designed pre and post activities can increase student learning significantly. Furthermore, tests are not used for assessment but as a way to further learning. Every time a student accesses the material in their memory, the memory changes so it is a stronger, more accessible and more stable.
This altering of the memory is in preparation for needing the knowledge in the future. Recalling the information causes more activity in certain areas in the brain that help stabilize the memories. It has been found that the more active these areas are, the better we remember the material.
Basically, retrieval practice is what makes the information stick in our brains. In addition, it helps us develop a deeper learning. The end result is that we are able to transfer knowledge from one situation to another. In fact, regular quizzes helps students perform better on unit tests.
Several other articles recommend that students continue asking questions on the material even after the section is finished so students have to work on retrieving the material. This continuation is referred to as spaced retrieval. Results indicate that spaced retrieval improves overall test scores at the end of the semester because they are able to access the information.
Keep in mind that space retrieval means students are being exposed to the material for briefer periods over a longer period of time. If you have finished slope, be sure to include quiz questions on the topic for the rest of the year so students have to access their memory.
So how can you change your teaching so you include additional repetitive practice over the school year so you are having students practice spaced retrieval?
Monday, August 22, 2016
Interleaving and Math
 Interleaving is making the rounds in the education community because it is so different from most of our teaching and the results indicate it helps students really learn the material even in math.
Interleaving is making the rounds in the education community because it is so different from most of our teaching and the results indicate it helps students really learn the material even in math.The idea behind this is simple. Instead of focusing on one skill such as learning piano scales, you mix the skills such as scales, chords, and arpeggios.
According to Scientific American, the advantages of interleaving include last effects, may be one of the most effective teaching methods for math, and strengthens memory associations.
By interleaving topics, the brain is constantly retrieving different responses to use in short term memory. Since each problem is different, the brain is creating connections between the different problems and the correct answers, it enhances learning. The drawback with this technique is that at first it seems the learning is slow and difficult at first, it produces longer lasting results.
It is suggested the types of problems be mixed up especially on homework to start the process. Although implementing it requires careful planning, it does not require extra training, special equipment or extra time which makes it fairly easy to use.
According to several articles I've read, the interleaving is best applied to independent practice problems and to homework because that is where it has the most effect. In addition, you might try to group problems according to related topics so there is a relationship. I do not mean have all the same type of problems but perhaps a ratio word problem with another for finding the slope of a line.
We often complain that students have difficulty in transferring their knowledge from one topic to another but this may help that issue since students are working more than one type of problem. The problems are mixed, requiring them to transfer knowledge.
According to Mind Shift At KQED, the question on home work is not about the quantity of problems but the quality of the problems included. They recommend mixing up the problems rather than grouping them by type so they don't know what the next one is going to be. This requires their brains to work harder finding the solution because they don't know what is coming next.
Various studies are showing that students who use this interleaving technique to help study the material end up having higher test scores than students who only work the problems grouped with the same type.
So think about this for the upcoming school year. When you assign homework, do not do the page 27 every 3rd problem. Select several from different pages and put them all mixed up on the homework page so students are given a more effective practice. This is what I plan to do next week, when I start assigning homework.
Let me know your thoughts. Keep an eye out because I plan to investigate other topics such as spaced practice, etc to see how I can use them in Math.
Sunday, August 21, 2016
Saturday, August 20, 2016
Friday, August 19, 2016
Thursday, August 18, 2016
First Day Activity
 Monday, school started. Due to the short periods, we didn't get a chance to do much and we are taking students out to camp for most of the week so I had to come up to an activity to ease them back into school.
Monday, school started. Due to the short periods, we didn't get a chance to do much and we are taking students out to camp for most of the week so I had to come up to an activity to ease them back into school.Since we have a break between Tuesday to Friday, I needed something because I do not want to teach until after our cultural event.
I created a 8.5 x 11 inch graphic organizer with 12 squares. The squares are labeled with 2 letters (A-B, or C-D) except for QRS and XYZ. I had the students divide into groups of 2 or 3 and gave each group a sheet.
The idea is that they list as many mathematical words for each letter as they can in say 10 minutes. At the end of the time, have students leave their papers on the desk, walk around looking at other peoples choices for a minute, then when they get back to their own desks they have 2 minutes to write down words they remember seeing.
Once they have reached this point, they are ready. I put the letters on the board and went around the classroom asking for words to go with the letters. I had the students say the word and then give a definition.
We had a wonderful time doing this. A student might say "Justify" for J and the explanation might be "Its the thing you make us do!" I questioned "Thing? What do you mean by thing?" We had a great time laughing due to those explanations the kids came up with while not really remembering the actual definition.
I enjoy this activity as a first day activity because it gently eases them back into mathematical thinking.
Wednesday, August 17, 2016
The Math of Japanese Balloon Bombs in World War II
 Another activity I had students work on during the cross curricular unit had to do with the balloon bombs Japan used in World War II.
Another activity I had students work on during the cross curricular unit had to do with the balloon bombs Japan used in World War II.There are so many possibilities for math with this topic.
1. These balloons traveled from Japan to Alaska, Canada, Washington, Oregon, all to way inland to the Great Lakes Region just using the Jet Stream. This article has a great map. Using google and math it would be possible to calculate how long it would take the balloons to travel from Japan to specific locations. The article states it took between 30 and 60 hours for the balloons to travel across the pacific. Students can also calculate the ratio of balloons reported versus balloons released.
2.Give the students the volume and diameter of the balloons and have them calculate how much material was needed to make the balloon for one and then for all the balloons. The balloons were 33 feet in diameter when fully inflated to carry 19,000 cu ft of hydrogen. At first they used silk but later used a specific type of paper. In addition, the balloon itself weighed 152 lbs.
3. The Japanese used sand for ballast in the balloons from a beach near Tokyo. Each balloon had 32 bags of sand weighing 155 lbs. Students could find the average weight of each bag of sand. Most balloons held one 33 lb bomb, four incendiary bombs (11 lbs each). In addition, each balloon carried 44 lbs of flight equipment. So how much weight was taken up by the sand, bombs and flight equipment.
4. The flash bomb fuse 64 feet and took 82 minutes to burn. How many feet per minute is that?
If you check this paper out, it has pictures and tons of technical information so you could create a worksheet of questions on this topic alone. Or you could assign groups to read the paper and prepare math questions for others to answer. This has tons of possibilities.
Have fun.
Tuesday, August 16, 2016
The Math of Tents
 I am getting ready to head out camping with the local high school
students. They will travel by boat down river, toward to ocean to a
small piece of land near the place this village was originally located
before it moved to the place before this one.
I am getting ready to head out camping with the local high school
students. They will travel by boat down river, toward to ocean to a
small piece of land near the place this village was originally located
before it moved to the place before this one.Have you ever wondered how math is involved with camping? I decided to check a few things out and finally found a wonderful piece on tents covering how they calculate the number of people each type accommodates to the various heights and other facets.
First of all, occupancy of a tent is based on whether it is designed for backpacking or for normal family use. For a backpacking tent, they calculate it based on the standard sized backpacking pad which is 20 to 22 inches and having people right up against each other tucked into mummy sleeping bags. If you are talking about a family tent, it is assumed that people need more space.
So a backpacker is said to need 15 square feet while in a family tent situation older teens and adults are allotted 25 to 30 square feet per person. This one fact leads to the rule of thumb of subtracting two from the rating of the tent.
It would be easy to have students go online to find their perfect tent for camping and use the figures to determine if the manufacturer used the backpacking or family tent square footage. This can lead to a discussion on the total tent floor space versus capacity and usage. In addition, students could sketch plans showing how people would sleep into the tent.
Furthermore, the article addresses how a non-rectangular shaped tent effects its capacity. Let's fact it. Rectangular tents are much easier to do calculations with because you can base those calculations on a rectangular body but if you have an hexagonal shaped tent, you might not be able to use the space effectively.
The final thing to know about selecting tents has to do with height of the tent. Some tents are designed for people to only sit in the tent while others allow inhabitants to stand. This leads to volume calculations for the tent. I use a small backpacking tent I can sit up in. I am extremely good at changing inside the tent.
So have the students choose a non-rectangular shaped tent for the same activity of calculating sleeping capacity, and designing a floor plan for arranging your family as effectively possible. The students then create a summary for comparing the tents and deciding which one they would buy complete with justification. They could even provide justification for why they chose a small tent vs a larger tent of vice versa.
Have a nice week.
Monday, August 15, 2016
The Math of Dunkirk.
 I am getting ready to head out on a boat trip so I thought I would share with you a historical math problem, applied to my locale. I think it was during my second year at this high school, the teachers got together to create a cross curriculum unit on World War II.
I am getting ready to head out on a boat trip so I thought I would share with you a historical math problem, applied to my locale. I think it was during my second year at this high school, the teachers got together to create a cross curriculum unit on World War II.You would think the math component was hard but it really wasn't. The hardest part was finding the numbers so the students could do the calculations.
One important event of World War II was the Dunkirk evacuation where a fleet of over 800 boats moved 338,226 men in an 8 day period while loosing 68,000 men. This lends itself to some wonderful math.
Students can calculate:
1. Ratio of deaths to survivors.
2. Average number of men moved per boat per day.
3. Average number of men moved per boat per hour.
Dunkirk is about 50 miles from Dover. There were actually three different routes that could be used but each had dangers, so I looked at an average. If you wanted you could have students calculate using all three distances for the problems.
I asked my students which village is about 50 miles away from here by water. Once we picked the destination, the students had to figure out how many boats would be available for use and the average number of passengers each boat could carry.
So for this project, students had to determine:
1. How long would a round trip take.
2. How long would it take to move 300,000 people using the boats available in the village.
3. What is the best way to set up the fleet so there is a continuous flow of boats moving because we are on a river that has to keep track of tides.
4. Could be house these 300,000 people in the village as they arrived.
5. Average number of men moved per day
6. Average number of men moved per hour.
Students were required to create a final write up with all the answers from the 6 questions. They had to include a map along with a write up and a conclusion answering the question "Could we have carried out this type of rescue?" They had to justify their answer.
Over the next couple weeks, I plan to share a couple other math activities from World War II.
Sunday, August 14, 2016
Saturday, August 13, 2016
Friday, August 12, 2016
Taking Bakers Math One Step Further
 Something Adam said the other day reminded me of a recipe I read many, many years ago. It did not list standard measurements. Instead, it used parts such as 3 parts flour or 2 parts liquid. This is a different way of looking at the measurements in cooking.
Something Adam said the other day reminded me of a recipe I read many, many years ago. It did not list standard measurements. Instead, it used parts such as 3 parts flour or 2 parts liquid. This is a different way of looking at the measurements in cooking.For instance, if you have a recipe for a spice mix calling for 1 tbsp cinnamon, 1 tbsp ginger, 1 tbsp nutmeg, and 2 tsp chili powder and you decide you want to create a recipe for a larger amount, you can use the parts method.
First I know there are three teaspoons in each tablespoon, so my basic part is equal to one teaspoon. So the ratio is 3 parts cinnamon, 3 parts ginger, 3 parts nutmeg and 2 parts chili powder. This is great because I can then decide that the part is the same as a cup and I can make up a huge amount using the same ratios.
I could also start with a Pie Crust recipe calling for 10 cups flour, 5 1/2 cups of cold butter, 1/2 cup water and 2 tbsp of salt. This type of recipe the base part is equal to 1/2 cup. I'd ignore the salt because its often just for the taste. So my flour is 20 parts flour, 11 parts cold butter, and 1 part water. So if I wanted to make the crust for a very small pie, the part is now equal to a tbsp or 20 tbsp flour, 11 tbsp butter and 1 tbsp water.
This is just a different way of enlarging or reducing recipes but did you realize the same type of idea is used in calculating the oil - gas ratios for 2 stroke engines? If you refer to a chart, you might see a 32: 1 ratio which means if you are using 32 ounces of gas you need one ounce of oil. It could also be for every 32 quarts of gas, you need one quart of oil
Something you need to know if you have a snow machine, ATV, Chain saw, or any other type of machine that is a two stroke. Some machinery is a 50:1 ratio or 50 ounces of gas mixed with one ounce of oil. As long as you know what the base unit is, you know how to mix things.
In construction, there is the 1:3 ratio for lime to sand mortar mixture. You could use 1 bag lime to 3 bags sand of the same weight. What about concrete which is 1 part water, 2 parts cement, and 3 parts sand so you could do 1 lb water, 2 lbs cement, and 3 lbs sand or it might be 100 lbs water, 200 lbs cement and 300 lbs sand.
It is so cool that ratios are used all over the place from baking to building. Have fun with this one.
This method keeps the ratios the same without having to mess as often with fractions and it shows
Thursday, August 11, 2016
Pokeman Go!
 Pokeman Go, the latest craze to hit the digital scene. It is an augmented reality app which has people running around malls, stores, and other places in search of Pokeman. Instead of being tethered to your x-box while you sit on the couch or lie on the floor, you have to be up and moving while searching for your quarry.
Pokeman Go, the latest craze to hit the digital scene. It is an augmented reality app which has people running around malls, stores, and other places in search of Pokeman. Instead of being tethered to your x-box while you sit on the couch or lie on the floor, you have to be up and moving while searching for your quarry.Pokeman Go relies on GPS to determine your location and know where to place the creatures for your hunting pleasure. This video by Kyle Hill give a very nice 7 minute introduction on the science and math of Pokeman Go. He has nice detailed information about the satellites and GPS used when hunting your prey!
The Stack Exchange has a lovely infographic on the three stats associated with the game. Two of the three base stats are hidden but all three are mathematically calculable with the equations shown. This infographic does a great job of explaining stamina, attack, and defense, the math that produces them, and how they relate to each other.
This Prezi presentation explores the mechanics and mathematics of pokeman from getting the perfect Pokeman to the amount of damage your opponent can take. The mathematics is specific and shown with excellent examples. In fact this Prezi explains certain material in the infographic with better detail.
What about moving up through the levels to 100. How long will it take you to do that? According to this article it takes as many points to move off of level 30 as it did to move from level 1 to 25 combined! There is a shop where you can buy additional balls so you don't have to spend the time needed to acquire them via playing. Think about all the fun you could have calculating probabilities for each level.
Speaking of the store and buying balls, there are things you can buy as a business which can drive additional folks your way. Since I've never played the game, I'm not as familiar with things like this but this article is written for the business owner. It gives hints on ways to get lures and find gyms which can drive foot traffic their way. I'd never thought about the economic possibilities on this.
You might want to integrate this information into your classroom and snag student interest in seeing how math is used in Pokeman Go!
Wednesday, August 10, 2016
What is Bakers Math?
 Have you heard of Bakers Math? I hadn't until I started reading my new book on Sourdough. It is a formula used by bakers who measure ingredients as a percent of the total amount of flour rather than relying on cups etc. Since they count the flour as 100%, the salt, liquid, and yeast are designated as a specific percent based on the ratio of the ingredient as compared to the flour.
Have you heard of Bakers Math? I hadn't until I started reading my new book on Sourdough. It is a formula used by bakers who measure ingredients as a percent of the total amount of flour rather than relying on cups etc. Since they count the flour as 100%, the salt, liquid, and yeast are designated as a specific percent based on the ratio of the ingredient as compared to the flour.One reason they use weight rather than cups is because each cup of flour does not always weigh the same. A cup of flour can weight between 115 and 155 g depending on how packed it is, the type of flour and if its been sifted. This explains why one time the recipe comes out beautifully while another time it might be too thick.
As a result of this inconsistency, bakers developed a formula which yields a more consistent product due to having a more precise recipe. Think about this, it's a real life application of percentages and ratios in a situation other than shopping and scale models.
The way it works is say you are starting with 500 grams of flour. The salt is 2% so that is 500 x .02 or 10 grams of salt. The liquid might be 70% or 500 x .70 or 350 grams of water while you need 1.2% yeast or 500 x .012 = 6 grams of yeast. I've seen recipes requiring anywhere from 60% to 80% for the liquid. If you add anything, it will be a percent of the flour. This requires 500 + 10 + 350 + 6 or a total of 866 grams of dough.
So how is this used? Its used in two different ways. First you are given the weight in pounds or grams and you want to know if the other ingredients fall within the accepted percentages. So if you have 100 pounds of flour, 60 pounds of water, 5 pounds of yeast and 2 pounds of salt. So you can easily figure out the percentages by division.
60/100 = .6 = 60%
5/100 = .05 = 5 %
2/100 = .02 = 2%
It looks like the yeast is a bit high so I'd consider reducing it.
You can also go the other way if you are given percentages and you need to find the weight of each ingredient. This is the math done in the example with the 500 grams of flour. So it is possible to use math to go either way.
This basic formula can be used to recalculate by knowing how many pounds or grams of dough your original recipe uses and the total percentages of all the ingredients for that recipe. To find your conversion factor you divide the desired new weight of the dough by the percent of the original recipe. Then multiply the percents by the conversion factor to give the new weights of each ingredient.
Lets look at this example. Your original recipe makes 150 lbs of dough but you want to readjust the recipe for 100 lbs. The percent of your ingredients adds up to 175.9% so you divide 100 by 175.9 which gives a conversion factor of .57 rounded. So you multiply each individual percent by the conversion factor assuming the flour is 100%.
Flour - 100% x .57 = 57 lbs
Water - 70% x .57 = 39.9 lbs
Salt - 2 x .57 = 1.14 lbs
Yeast 1.2 x .57 = .69 lbs
So this gives about 100 lbs.
If you want to see this type of math in more detail check out King Arthur's Flour website. It has great examples and I'm going to throw a couple of these in class for warm-up. Hope you find this interesting.
Tuesday, August 9, 2016
Prime Numbers
 If you asked your students to describe what makes a prime number
prime, most of them will either shrug or tell you its a number whose
factors are one and itself. If you ask them to draw it, how would they
react? Mine simply would shut down because they have no idea how to do
that.
If you asked your students to describe what makes a prime number
prime, most of them will either shrug or tell you its a number whose
factors are one and itself. If you ask them to draw it, how would they
react? Mine simply would shut down because they have no idea how to do
that.I read a cool book called "The Joy of X" by Stephen Strogatz in which he presents prime numbers in a way I like. Think of a prime number as a number than can be expressed as a square or rectangle no smaller than 2 by 2 with no left overs.
By this definition, it is easy to draw prime and composite numbers and it makes it easy for students to see why one is easily factored while the other cannot.
If you look at this first picture you will notice that it is not until you get to four that you have a 2 by 2 shape - a square. This means that 2 and 3 are prime numbers because they do not form the right shape.
Now look at the following illustrations for 5, 6, and 7.
Notice that the drawings of composite numbers also illustrate at least one set of factors. The factors of 4 are 2 because 2 x 2 is 4 or 4, 1 because 4 x 1 is 4. Where as the 5 shows no nice factoring and that makes it easy to tell it is a prime. For larger numbers, this is where the rules of divisibility come in or factoring trees.
I really like the way Stephen explained it because it gave me a way to help my students "see" a prime number as more than a definition.
Monday, August 8, 2016
Area Maze Apps
 I would like to start out by thanking Josh Fisher for turning me on to this and to Sarah Carter at her Math Equals Love Blog for explaining Area Maze.
I would like to start out by thanking Josh Fisher for turning me on to this and to Sarah Carter at her Math Equals Love Blog for explaining Area Maze.Rather than search the internet for websites, I looked for iPad apps and found at least two free ones to review.
The first app is by Wasabi Applications and its called Area Quiz. The idea behind this game is that you are given a figure with missing information. Using logic, you determine the missing value but the value might be the whole area, part of the area, or a side measurement. The problems are not always easy.
When you turn on the app, this is the screen that appears. Notice the unit is cm^2 because this app was created by a company that uses metric. Once you tough the play button you are taken to the second screen.
The second screen indicates there are 5 different levels to work through. You cannot move to another level until you have acquired a certain number of stars. Note its only 10 to unlock level 2 but it increases with each level so it requires additional work.
I am on level one number three. Note the picture, you are expected to find the area of the shaded part. It requires thought to figure out the two missing measurements. You type in the answer and hit enter.
If your answer is correct, you get a start and move on. If it is wrong, a huge red X appears and you cannot move on till you get the correct answer.
The other app is Area Maze marketed by Happy Meals which is just as good but some of the problems are a bit trickier.
This is the front screen when you open up the app. Notice much is in Japanese but the directions and numbers are in English.
As
far as I can tell, there may be more levels but I have not worked my
way through this. I got as far as number eight before I got stuck.
When you do it and you are correct, you get a beautiful green area but
if you are wrong, it plants a huge red X and tells you to try again.
This
is the one I am stuck on. This app varies from the other because of
the timer that ticks away as you work on the problem. As I was writing
this, I realized I was looking at the whole thing from the wrong angle.
I checked my answer and I was right! Yeah.
I
plan to put these apps on my iPads. When they work the problems, I am
going to require they sketch out the problem and show how they solved
it. This gives them a chance to practice explaining because many of the
new tests require they show their thinking.
Check them out, they are both free.
Sunday, August 7, 2016
Saturday, August 6, 2016
Friday, August 5, 2016
Air Traffic Controllers and others.
 As I wait for my delayed flight at SeaTac Airport, I watch all the planes that land and take off in a constant stream. Do you realize that a handful of people direct these planes much like a choreographer who plans a dance?
As I wait for my delayed flight at SeaTac Airport, I watch all the planes that land and take off in a constant stream. Do you realize that a handful of people direct these planes much like a choreographer who plans a dance?Who monitors and directs this dance of planes. First there are the Air Traffic Controllers who monitor the landing and take off of all planes. They have to control multiple paths of approaching and departing traffic.
On the other hand, schedulers determine which plane goes to which gate and which people will work on that flight both pilots and hostesses. They also determine the routing each plane take between airports.
I wondered what math is required by Air Traffic Controllers to do their job. It is obvious they need to know the speed of the jet so they know where they are and how long they have before they land. So right there is rate x time = distance.
Is there other math? Perhaps the Pythagorean theorem, angles of decent, distance required to stop in, juggling the approach of multiple aircraft or knowing wind direction because that sometimes effects landing. In order to be an Air Traffic Controller, people are expected to have a degree and to have taken College Algebra, Trigonometry, Geometry, Calculus I and II, Statistics, which is quite a bit of math.
They have to monitor a circular radar grid to keep track of airplanes with the tower at the center of the circle. Their location is identified by distance and angles. The vertical distance of a plane is the distance between the plane and the ground which is important. They combine all of this information with weather conditions and speed to plot their path.
Each airline has schedulers who have the responsibility of determining which airplanes use which gates, create the schedule for crew, and determine the actual route the air plane takes between takeoff and landing and work in maintenance. This looks like a real life applications of combinatorics much like those questions "How many different combinations do you have if you have 4 pairs of pants, 3 shirts and 4 hats?"
Most of the sites that spoke of the math involved in scheduling turns out to be calculus, there is a nice 8 page pdf which discusses simulating the cost of moving planes around the airport from gate to maintenance, fuel and operating costs, etc. This paper provides the results of the simulation and at the same time gives out some real information on scheduling.
Although this Power Point presentation is designed for the industry, it has some wonderful slides which explain each part of the process and has a flowchart showing the overall departmental arrangement and work distribution.
I could not find any simple lesson plans for scheduling airplanes but I found enough information to create a simple combinations activity using planes, crew, towns, and flight paths. I hope to create an activity in the next month and post it here to share with people. Please keep checking my site out for this. Next week Tuesday, I'm looking at the math involved in the newest craze Pokeman Go! Stay Tuned.
Thursday, August 4, 2016
Does Standardized Testing Really Show A Person's Knowledge.
 I just spent the weekend in Los Angeles talking with several different people at a conference. The topic of teaching and testing came up. One gentleman who is a local teacher said his school beta tested one of the Smarter Balance Tests.
I just spent the weekend in Los Angeles talking with several different people at a conference. The topic of teaching and testing came up. One gentleman who is a local teacher said his school beta tested one of the Smarter Balance Tests. He noted many sections presented information but the questions did not use that information. He also stated that many of the questions used methods that are not normally taught in class.
He wondered why we teach box and whisker plots or stem and leaf plots because he's never seen them used in real life. He worked in industry before he became a teacher and in all that time, he's only ever used histograms. These two observations lead to someone who spent 40 years working for the FAA add most people are not required to know all the material in their head. They are allowed to work with others, look up information, or check to make sure they have it set up right.
It was acknowledged that tests are used to check for a person's basic knowledge in the case of a person who wants to become a lawyer, CPA, or Nurse but once they are done and have their credentials, they don't have to take the test again unless they move to another state. Yet we are now testing students every year.
I hate standardized testing for several reasons.
1. Many places use only the results from standardized testing to determine if a school district is progressing nicely.
2. Special education students are held to the same standards as those without a learning disability. Even with accommodations, students may not have the knowledge to pass these types of tests.
3. Many questions are not culturally appropriate. I've seen questions showing a student who rides a bus to the mall to shop for a coat. There are no buses in my village and their clothing is usually ordered from a place online. They do not relate to this.
4. A student's results vary from day to day depending on so many outside factors such as are they sick? Did they get enough sleep the night before? Have they regularly attended school? Is their understanding of the English language good enough to understand what is being asked?
5. Results from the standardized tests are sometimes used to determine where students need improvement. Unfortunately, the standards are being tested vary from year to year so what was tested last year may not be the same ones tested this year.
6. Multiple choice math questions for the most part only tell us which questions students got correct, the questions do not tell me what part of the process the student still has issues with. It doesn't tell me which problems they don't even know how to do.
If I am going to use standardized test results to help determine what I teach, I'd rather use them them as one part of results I use. I spend time in my class teaching students ways to take standardized tests such as elimination, underlining key words, etc. I even work on teaching appropriate vocabulary such as Justify, Elimination, etc. They have to understand what they are being asked to figure out the first step in solving problems.
Wednesday, August 3, 2016
How Our Brain Processes Problems.
 I regularly receive a newsletter from the National Council of Teachers of Mathematics filled with lots of information about studies, new information, and other things to help me stay up with current trends.
I regularly receive a newsletter from the National Council of Teachers of Mathematics filled with lots of information about studies, new information, and other things to help me stay up with current trends.The article is from the New York Times. They reported on a study done to see how the brain works while solving mathematical problems. They studied results from two different tests. The first recorded the images of neurons firing in the brain while the other focused on how the patterns shift over time as problems are solved.
Using the results, scientists claim there are four stages involved in solving math problems. The first stage is encoding or downloading occurs when they read the problem. The second stage is planning or deciding on the strategy needed to solve the problem. The third stage is solving it or actually doing the mathematical calculations and the last stage is responding to the problem or writing down the answer.
This study looked at how the type of problem effected the duration of each stage. Some problems took more time to plan and less to solve while others took lest time to plan and more to solve but both problems might take the same amount of time to complete from start to finish.
In other words, this is the first time they've been able to observe the internal process the brain goes through when solving problems. The authors of this study are hoping to figure out how the brain works so they can determine a way to help students learn to ignore extraneous distractions to focus on the math program.
These stages correlate to how I teach students in the classroom to solve math problems, especially word problems. I tell students to read the problem which is encoding or downloading the problem into the brain. Next is to plan how to solve the problem or the second stage when you choose a strategy be it draw a picture or guess and check. The third stage is to do the calculations and the final is write down the answer.
This study provides the first answer to the question of how does our brain work when it solves math problems. So with future investigations scientists might soon take this information and formulate cognitive theory so we can develop better ways of teaching students.
Tuesday, August 2, 2016
Snowboarding and Bikes!
 Think about it! Snowboarding is an Olympic sport and has been since 1998 when it was added as a totally new sport. I have a nephew who regularly headed up to the mountains to snowboard every winter. If I asked him what math is involved with snowboarding, he'd either shrug or give me one of those looks. You know the one where he thinks I'm crazy because we are not in the classroom and everyone knows you don't do any math outside of the instructional period.
Think about it! Snowboarding is an Olympic sport and has been since 1998 when it was added as a totally new sport. I have a nephew who regularly headed up to the mountains to snowboard every winter. If I asked him what math is involved with snowboarding, he'd either shrug or give me one of those looks. You know the one where he thinks I'm crazy because we are not in the classroom and everyone knows you don't do any math outside of the instructional period.Well, guess what. There is quite a bit of math involved from angle of approach, to drop, to rate/time/distance to slope. A nice introduction to the whole topic is this Prezi. In addition to listing the math, it gives example problems to illustrate their point. I enjoyed watching it myself especially as I do not snowboard or ski.
This little problem from Bed Time Math has a lovely video showing a crow snowboarding using a lid. There is a question to go with it that you could use or you could make your own
Did you know there is an actual formula for finding the right length of a snowboard to go with your height? I certainly didn't. Based on this entry, the formula is basically 88% of your height in centimeters. The 88% is actually an average based on the recommendation of 85 to 92% of your body height. In essence, that makes it a real life application of a proportions and averages. This formula is used to find the starting point because there are other factors involved.
According to The House site, weight is actually much more accurate than the height and they rely on a chart but they also have a wonderful page that talks about bindings, types of snowboards, etc. It is a very comprehensive site. I'd like to thank Kate from here for answering my questions.
Now on to bicycles! How about starting with this Power Point Presentation that introduces students to the math of cycling. It covers speed, gear ratio, angles of the frame, and wheels. The information is detailed with explanations and examples. If you want to take this a step further by focusing on BMX bikes, this site explains specific gears, cadence, wheel size, and angles involved in the actual sport. The two together provide a good introduction to the topic.
Now how about some hands on math using bicycles in two different ways? First this activity has students investigating and analyzing bike tracks at a crime scene? You set things up and they have to do the work. The lesson is arranged to take them through the process step by step.
From PBS comes two different activities focusing on upper elementary and middle/high school levels. These activities investigate a variety of bicycles to answer the questions. This is great if you have access to all the types of bikes but if you don't, you could adjust the activity to change it into a research project so students have to search for the answers. They gain researching skills.
I wanted to look at the math associated with bike tricks but I could only find a pdf on the mathematics of bicycle tricks but it is a heavy duty paper with more variables than I've seen since I was in college! It has computer models to show the steps involved in a variety of tricks otherwise, I can't find anything. It gives students the idea that the math is not simple.
Finally, if you want to create a full unit, check this one out. It takes the students through tangents, circles, motion, rate of change, simple machines, in addition to four weeks of experiments to add the hands on component to the unit. Its put out by Yale and has everything needed to make it your own.
So here are two sports that students love to do and using it to teach math might grab their attention and help them see the value of math.
Monday, August 1, 2016
Why Must All Students Be College Ready?
 When I was in high school, I went to schools both in the United States and in Australia. At that time, there was a belief that not every child wanted to go to college.
When I was in high school, I went to schools both in the United States and in Australia. At that time, there was a belief that not every child wanted to go to college. It was interesting because at that time, it was believed that we should prepare students for either college or for going into the work force. That was the key word - prepare.
I spent two years in Australia which was way different than in the United States. At that time, students in 8th grade, chose a strand for either college bound, office or work, or life skills. The difference was that there was one strand in the office or work tracks that allowed students to choose either college or work at 16.
16 was the magic number when you left school or you took classes to prepare you for college. There was this little law that allowed employers to pay young adults between 16 and 18 less than adults so many would hire someone just out of school and fire them at 18.
It didn't matter which choice a student made, they were taught the appropriate math be it algebra or accounting or math associated with carpentry or cars. I knew several students who studied shop or office subjects while planning to go to college so they would have a choice.
In the United States, they offered a distributive education designed to have students work half a day in a real business while taking English, Math and Social Studies. This a a place where many students left school to work in the oil fields because their fathers worked there and it was a way to support a family. Many girls started families before school ended.
The commonality between these two ways is simply based on making sure students had a choice, training and no matter which way they went, they were taught math. It might have been the math needed in the working sector but it was math.
Recently, we are operating under the idea that all students should be prepared to attend college rather than think about becoming plumbers, carpenters, office workers, etc. The people who keep society functioning! Think about it! People who make sure everything moves smoothly.
I love teaching math. I love integrating technology into math. I love finding mathematical applications of the math I teach but I wish I had the time to spend showing the wonders of the world of math to the students.
Some students need the choice because without it, they feel helpless and are less likely to buy into learning the topic. Choice of their future. Choice makes a difference. Choice.
Subscribe to:
Posts (Atom)