Two Truths and A Lie

Two truths and a lie is a nice quick activity easily incorporated into the math classroom and it can be used in several different ways.

Two truths and a lie is where you create two true statements and one false.  Students need to identify the false statement.

The two truths and a lie can be used by themselves or with some sort of illustration like a picture, photo, or infographic.  As long as two of the statements are true and one false you are fine.

This activity could be used as a warm up to get students into the mathematical mindset.  Here is an example.
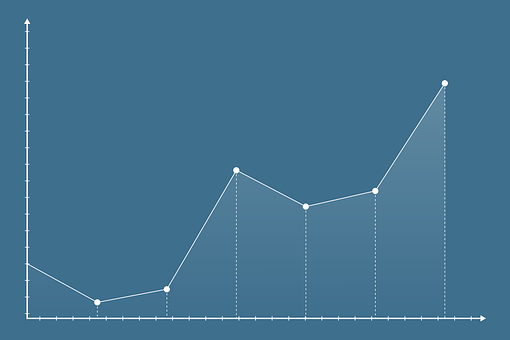1.  This line graph indicates mostly growth.

2.  All the points are equally spaced apart.

3.  Temperatures on one-third of the days dropped.

Which statement is the lie and justify your answer.


If you have students justify their answer it helps improve communication skills and could possibly lead to a classroom discussion among the students as they justify their answers.

Another way to use this is to put something up so each student can create their own two truths and a lie based on that picture, problem, or diagram.  Once everyone is done, have them post their two truths and a lie on the wall to share with others.  This can be taken a step further by labeling each entry with letters before having students choose the lie for every product. Once everyone has made a choice for each product, the students can share their answers with the others.

Instead of doing the two truths and a lie, prepare an equal number of truths and lies to post around the room.  Let students look at each statement before deciding if the statement is true or false and they should include justification for their answers.  Suggestions include things like "When you multiply two odd numbers you will always get an odd number."   which is not correct.

This activity can be used with mathematical vocabulary so that there are two true statements and one lie for each word.  Students have to identify which one is the lie and justify their answer.  An example might be:
Product

1.  It is the result of two numbers being multiplied together.

2.  It is always larger than the two numbers multiplied.

3.  If you multiply two odd numbers, the product is always even.

There are so many ways to use this activity in class that you are restricted only by your imagination.  Let me know what you think, I'd love to hear.  Sorry about skipping yesterday but I spent most of the whole day, catching up on sleep.  I should be back to normal.  Have a great day.

Interest rates

I have not posted the past few days due to attending an educational conference and I was busy from quite early to quite late.  As I sit in the airport, waiting my flight to Alaska, I checked out today’s issue of USA Today and discovered something that I didn’t know about.

Most of the time when we discuss interest rates, we use current market rates and we apply them to standard situations. I appears that interest rates can be much higher under certain circumstances, especially for those short term loans.

Apparently, there are several companies who loan money to desperate people but they end up charging anywhere from 200 to 500 percent.  Yes, I know rates are not supposed to be that high but companies have discovered if they can associate themselves with native tribes, they can charge more interest because they are no subject to certain rules.

These tribes are not involved with the actual loans but they provide the protection via their immunity from governmental interference.  The whole point though is that many people fall prey to these companies. So it might pay to have students create spread sheets to calculate the total amount of interest using current rates, rates charged by these companies and other short term paycheck loan businesses to see how these differences in rates effect the total amount spent.

My plane is getting ready to load so I am off. I will be back to normal tomorrow.  Have a great day.  Let me know what you think.

Planning for a Substitute.

I recently read that it is important to have detailed lesson plans so if you are sick, you don't have to come in to make lesson plans for the substitute.  The place I last worked required teachers to have a substitute book complete with attendance sheets, lessons, etc so if you were suddenly out, there was something for the sub to follow.

I do not like having a sub trying to follow my lesson plans, detailed or not, because most of them barely have a high school diploma.  Usually, I'm lucky if the sub even follows the directions I've left behind so I hate being out.

I love it when I'm able to use something like Google Classroom as part of the daily routine because I can post everything to it for the students and send a quick note with lesson plans to the school secretary or another teacher.  This way the sub has general lesson plans but I've been able to post the specifics in Google Classroom.

I can post warm-ups, videos, work, everything so that students do not loose time because the sub has trouble following written directions.  When I am gone, I love posting links to annotated videos because these often have questions or reminders for students.  They can also write down notes in their notebooks and I don't have to be there.

I can also post links to work such as in Thinglink or post a hyperdoc which leads them through the basic material.  I love that the internet now has lots of quizzes or activities which are interactive.  By interactive, I mean students type in the answer and they get immediate feedback while I get information on which questions students missed and which they got correct.

If I know I am going to be out several days and I'm not sure if they can handle the new material while I'm gone, I sometimes assign a project such as creating a math tour of mathematically significant buildings, or investigate musical compositions based on pi or research mathematicians.  For the last, I'd set up google slides where students post the information on the mathematician so at the end, we could turn the slides into books.

Another thing I like to assign are certain internet based mathematical games for students to play and write reviews.  The reviews should cover the aspect of math the game focuses on such as in Angry Birds, you are working with parabolas,  how the game is played, and what they think of the game and why.  The last thing they would do is to explain how the designers could make the game better.

One thing I keep in the room for those days when I cannot plan ahead, do not have access to the internet are episodes of the old TV series Numb3rs because I can still find activities to go with each episode on the internet.  I can have the sub show the video one day and the next have the students work on the activity.  Early in the year, just before school starts, I take time to write guided notes they can fill in as they watch the video so they know what is important.

Usually I keep emergency lesson plans around but once in a while something happens and you do not have time to prepare.  About a year and a half ago, I got a call that my sister was in the hospital, possibly dying.  I got out of there but because of Google Classroom, I posted daily assignments, answered questions, etc without freaking out about not leaving proper lesson plans.  It made life easier.

I love the digital era in that it does make life so much easier in regard to subs.  Let me know what you think, I'd love to hear.  Have a great day.

Improving Vocabulary in Math

Vocabulary plays an important part in the math class because if a student does not understand the meanings, they will struggle.  Unfortunately, just copying out the definitions doesn't mean much because copying does not require students to really think about the meaning.  It is much more effective if they can define it in their own words.

There are many ways to help students learn vocabulary other than by copying words and their definitions.

One way is to create a word wall with examples of what it is and is not, a picture, and a definition in their own words.  Students create everything to go with the word.  The words on the word wall can then be used in different activities such as creating statements about the words that students have to decide if they are true or false.  Or make statements using always, sometimes, or never such as "two odd numbers added together make an even number."  which would be always.

A similar activity is to have student go on a word hunt looking for the words in a specific part of the book as a pre-reading strategy.  They look at the word, decide if they understand it or if it needs to be clarified.  If they need more info on it, they can add it to their questionable list.

Have students create vocabulary cards with the word on one side and place the definition and a picture on the other side.  All students use the same word list.  Once everyone has a card done for each word, divide students into two groups.  One group makes a circle while the other group forms a circle on the inside facing the other group.  The outer group holds up a word for. the other person to define, then the inside group chooses a different word and shows the definition for them to come up with the word.  The groups move so each person has a new partner, repeating the process.

Always discuss the multiple meanings of words such as product.  It is always a good idea to have students brainstorm meanings for the words and then discuss all the meanings within their proper contexts so students understand them better.  This is especially important if you are dealing with English Language Learners because it helps build a better language foundation.

Have students find places outside of school where the words are used.  They just can't say they saw it, they have to provide proof.  So if they see a sale poster offering something at a 35% discount, they could take a picture of it and share it with the class or email it to the teacher.  This gives them a chance to see the math used outside of the classroom.

Pass out stacks of vocabulary words to groups of students and let them divide them into categories.  Once they are done, they explain how they divided up the words and the categories they used to classify the words.  This way, there is no one right way and it allows students a chance to use higher order thinking skills.

Give each student a vocabulary word and let them create a cartoon with the definition, picture, examples and non examples.  Create a digital version with all of the cartoons to share so everyone has all the cartoons.

Final advice is to always use the vocabulary in the class so students get used to hearing it in context.  It does not help to have students learn the mathematical terms if you are not going to use them in class.  Let me know what you think, I'd love to hear.

Lesson vs Unit Plans

Too often, teachers run out of time and loose track of the unit plans, focusing instead on the day to day lesson plans.   Units are the topics connected by a common thread while lesson plans are for one part of the unit.  Units take two to three weeks while lesson plans are taught daily.  By looking at the unit topics first, it makes it easier to plan the lessons so the material is covered in the correct order.

Unit Plans should have the topics, skills needed, desired outcomes, standards they meet, connections to other topics or real life, links to big ideas, identify past learning that connects to current learning, questions for daily learning, expectations, necessary vocabulary, and planned assessments for pre, during, and post unit.

It is suggested one create an outline beginning with the academic goals for the unit.  It helps to identify what students know and what they should know at the end of the unit, determine how long it will take to cover the material, and then select the textbook pages and other materials needed to teach the unit. The idea is to enhance learning.

The lesson plans are what is used to teach students the material of the unit.  It is suggested teachers plan each lesson with complete detailed information so they know exactly what they are teaching and what the students are expected to learn each day.  In addition, the detailed lesson plans are easy to implement by a substitute should the teacher be absent.

Furthermore, the lesson should be designed so students know why they are learning the material and it should have some sort of hook to capture their interest.  There should be something to check on what they already know before teaching the lesson.  Before teaching the main lesson, teachers should check for misconceptions by activities such as having students look at problems done incorrectly and then identify what was not done correctly.

One thing that is often suggested is to have student learn to do the problems using guided practice before having them work independently.  At the end of the lesson, review, recap, and bring the lesson to a close.  The lesson plan should include how much time is being spent on each part of the lesson along with specifics of the activity.

It is also important when teaching vocabulary to include both mathematical and non mathematical meanings.  Furthermore, one should use and reuse the vocabulary through the unit so that students learn the meaning and are able to use the terms properly.

When you give students time to brainstorm, do warm-ups, or other type of activity, it has been suggested the teacher use a timer so the lessons keeps moving instead of dragging at points and not covering everything that day.

Let me know what you think, I'd love to hear.  Have a great day.

Good Lesson Plans

 It is so easy to find lessons on the internet for various topics in Math but not all of them are good.  In addition, schools either have exact forms they want you to use for your lessons or they leave it up to you.  My last school left it up to me, so I threw everything on a spreadsheet for the week with few details only because it wasn't demanded.

I have books on differentiating lesson plans, universal design, backward design, and just about every other hot topic but what things do you want in a lesson plan to make it a good one for math.  The first thing to remember about writing a good lesson plan is that each lesson is connected to larger topic so things should not be taught in isolation.

Although most of us are given math books complete with pacing guides, quiz and test books, and everything else we need, they don't always include ways the topic is connected with the real world, or tied to other subjects.  The books tend to teach topics in isolation.

It is always good to start the lesson with a warm-up or a bell ringer to help get students into a "mathematical" mindset.  This is where I use open ended questions or ones that require higher thoughts.  I love Esti-mysteries by Steve Wyborney because the kids end up quite involved.  He is also the inventor of "Splats" which also require some higher level thinking.

Next is the direct instruction to introduce new material or review previously taught material.  Although we want students to practice learning things on their own, it is important for teacher to include direct or explicit instruction.  it is recommended you do not spend more than about 15 minutes with this part of the lesson or students will begin to tune you out.

One thing many teachers forget is having students read the textbook before teaching the actual lesson.    Many students arrive in high school without learning to really read a textbook or if they have read textbooks, they've read them the same way you read a textbook in English.  They start at the beginning and go to the end of the section.  It is worth taking time during direct instruction to teach students how to read a math textbook and practice it through the year.

After this students practice the topic but not necessarily with a lot of closed problems.  Practice should include scaffolded instruction using manipulatives, one on one instruction, peer tutoring, or small groups.  As they become more confident, then move the assignments to being more pen and paper.

Then students should work independently or in larger groups to complete the assignment.  This is where you might give each student a problem to complete and include an explanation of how they did the problem on google slides or even flip grid.  This is also the part of the lesson where the teacher might ask students how they arrived at an answer, what was difficult about solving the problem, or could they convince the teacher the answer is correct?  Be sure to include open ended problems so students can move past simple solving into including communications.

Finally, finish with a time of reflection which could be done via some sort of math journal.  The reflection for the student might include questions on how they think it might be used in the real world, or to discuss what they still don't understand, or what they had trouble with.

During both the independent or group work, students should be practicing their communication skills.    This means they need to practice expressing ideas both verbally and in written form.  If they cannot explain it using either, then they really do not understand the material as well as they should.

Once the lesson is taught, the teacher should go through and reflect on how well the lesson went.  There are always things we can fine tune to make the lesson better and more important.  Let me know what you think, I'd love to hear.  Have a great day.

Something Different.

When Do We Go Back?

Historic Moment.

50 Years Ago We Landed On The Moon.  Celebrate!

The Cost Of Going To The Moon and Related Topics

50 years ago tomorrow, the United States landed men on the moon.  The total cost of getting them there and the subsequent rockets ran $28 million between 1960 and 1973.  If this amount were readjusted into today's money it would equal $288.1 billion That is quite an increase.

The actual cost of sending Apollo 11 cost the United States $355 million which in todays dollars would be $1.3 billion in 1994.  Of the $355 million, $200 million was spent on the construction of spacecraft and its equipment.

The original cost of the Apollo program began at $7 million but eventually jumped to $20 million, ending at the $28 million.  At the peak of the program in 1966, the Apollo program used 60 percent of the $5.2 billion budget.

In the meantime, Trump has declared that we need to get people back to the moon via the Artemis program.  The cost is estimated to be $30 billion to make the deadline of having them there by 2024.

This cost includes recruiting companies, building a lunar space station, and landing people on the South Pole of the moon.  The idea is to get people on the moon first before heading off to Mars.  There is a question as to how accurate that amount is because NASA spent $104 billion for the Constellation program that never actually left the ground, or the space station that is estimated to have cost $100 billion to this point.

This article has lots of figures, statistics, and information.  It is a good one to have students read and decide which ones are important and which ones are not as important.  It also have a lovely graph showing the break down of costs by year devoted to the landing vehicles, space craft, development and operations, ground facilities, and other projects.

On the other hand, there are collectors out there who collect anything dealing with the space program and pay the most for items associated with Apollo 11.  Sotheby's is holding an auction of space items which they expect to get quite a bit of money from.  For instance, they expect three bundles of magnetic tape from mission control in Houston to fetch between $1 million and $2 million because they are the earliest and sharpest material.  In addition, a copy of the Apollo 11 flight manual is expected to go for around $9 million.

That gives you an idea of how much it cost to get man to the moon back in July of 1969, the cost of the program, the cost of the upcoming program, and what space mementoes bring on the market.  It' s easy to figure out questions that use this information. Let me know what you think, I'd love to hear.  Have a great weekend.  I'll be back to normal topics on Monday.

Generalizations in Mathematics

We find a lot of generalizations in math but most students have difficulty in looking at generalizations and applying them to different situations.  For instance, multiplying numbers and multiplying binomials are the same process so if you know how to do one, you can do the other but most students see them as totally different.

By definition, generalizations are patterns that are always true. It is taking ones observations to create conjectures based on those observations, so they can be applied to the same type of situations.  An example of this might be that when two odd numbers are added, the resulting number will always be even.  This is a generalization because it is true for all cases.

Many math teachers do not take time to identify generalizations when teaching them.  Generalizations can involve either processes or products.  There are three components to generalization - expansive, reconstructive, and disjunctive.

Expansive refers to expanding the existing information of the student without changing what they already know.  This means the new information is close to what they already know.  In addition, if this information is close, students often reconstruct their cognitive knowledge.  Disjunctive is when a student uses disconnected pieces of information put together to provide the generalized knowledge to solve new problems.

The process most students go through begins with specific problems to formulate conjectures, which are then symbolized before arriving at generalizations.  Generalizations help students jump from what they already know to incorporating new material into their understanding by providing a link.

The thing about generalizations in math is they should start in Kindergarten so by the time they get to middle school and high school, they are accustomed to working with generalizations.  Many times as we teach general formulas such as (a + b)^2 = a^2 + 2ab + b^2, students have difficulty connecting this with a problem such as (x + 3)^2.  In addition they don't always recognize x^2 + 3x + 9 as factoring to (x + 3)^2.  The formula is the generalization while the (x+3)^2 is the specific application.

So as part of the mathematical programs, we need to spend time helping students learn generalizations either through direct instruction or through the use of manipulatives so they can then apply the generalizations to specific situations.

One way to help students learn to make generalizations is to use open-ended problems and tasks.  Once students have made a generalizations, they need to answer the questions "Does it always work?"  and "How do I know it works?"

One example of an open ended task is to provide students with 12 addition and subtraction problems.  Some of the subtraction problems might be 12 - 5 or 7 - 11 while the addition problems might be 12 + 3 or 7 + 0.  Have them group the expressions according to their own rules.  When students are done, write down the different ways the groupings occurred and see if students can then create their own generalizations, ending with the two questions.

Another one might be to come up with a variety of shapes that all have the same areas and have students divide them into groups.  Repeat the write the criteria they used on the board and see if they can come up generalizations.

So look for ways to encourage students to generalize so they can learn the material better.  Let me know what you think, I'd love to hear.  Have a great day.

Dynamic vs Static Learning

 As more and more technology is brought in the schools, we need to change how we teach children in school.  For decades, static learning was the standard model used in classrooms.  Static learning has students filling out worksheets, even digitized ones.  In other words, they are not interactive and there is only one way to complete the activity.

In static learning, you only have to write the assignment once and you can use it again and again.  It never changes.

Dynamic learning is more interactive in that it requires collaboration, creation, and communication.  It can involve others beyond the school buildings or interaction with others.  Dynamic learning might involve watching annotated videos, explaining in a video or flip grid, write an interactive book and publish it online.

Dynamic learning are assignments that change and evolve as research and technology evolve.  In a sense it grows and changes to meet the needs of the students.  This form of learning also allows expects you to use data to change the assignment based on student work.

The static vs dynamic goes beyond the types of assignments used.  It can cover assessments too.  Most textbooks come with accompanying tests and quizzes you can download or copy which are static because they are always the same.  A step up is being able to create a quiz or test from a bank of questions.  Furthermore, most of these are designed to determine what students don't know rather than what they know.

What makes assessment more dynamic is if the mode helps students show what they have already learned.  One way of doing this is to listen to the student explain what they are doing.  Just by listening, you can tell so much and its very dynamic because what you hear will change as they learn.

Another way of dynamically assessing students is to come up to a group and just listen to their conversation to determine what they understand and to observe their interaction rather than interrupting to ask them to explain their thinking. Often times by just listening, you learn more about their thinking, not just what they share with you.

In addition by observing the interactions among the students it is possible to tell if one person is doing all the work while the others sit back or if everyone is involved.  It is possible to listen in on explanations between pairs of students.  Unfortunately, as teachers we learn to pair a strong student with a weaker student to encourage learning but it does not always work out that way.  Sometimes this model encourages a learned helplessness of the weaker student and the stronger student gets frustrated while other times it   By observing and listening, the teacher can determine if the pairing is the right one.

The biggest difference is that static has a much longer existence than dynamic because it doesn't change.  Unfortunately, people often think if you digitize an assignment, it makes it dynamic which is incorrect.  If however, you place a problem on a Google slide for each child and then have them do the problem and bring in a video to explain the problem, this is dynamic.

Let me know what you think, I'd love to hear.  Have a great day.

Review of Maphi

The other day I stumbled across an app that is new to me.  It is call Maphi and it works on helping students learn to do the process of solving  problems by moving terms around to eliminate them as in moving a negative to its positive results in zero or canceling fractions

The app is free and has students work their way through the tutorial so they learn more about how the program actually works.











 The tutorial section has students review basic arithmetic, variables, working with negative numbers and basic fractions.  Each section has you work through problems

In addition to the tutorial section, students work through the distributive law, fractions, and linear equations.

Each section is broken down into smaller topics so students can work through each one with immediate feedback, hints, and it prints each step at the top for the student. 

Then at the end of the topic, there is a final test covering everything they worked on.

Example of a problem with negatives.

Distributive property subtopics

Fraction subtopics and prerequisite needed before attempting this.

I am not sure how I feel about just moving terms around to work through it but I do like the immediate feedback and it is based on gamification.  I do like the way students work through the problems with hints and a record of what is going on.

If you've used it, I'd love to hear your feelings on this app.  Have a great day.

The Math of Pizza

If you read my warm-ups over the weekend you noticed they dealt with the cost of making a pizza vs the price its sold for and the amount of mark-up.  It's important to realize the numbers used may not be the same in your area.  In Alaska, many things cost a bit more because they have to be shipped up here.

There are other ways to include pizza into the math curriculum such as when looking at unit prices.  One cannot compare a small pizza to a large pizza by price.  Its much better to figure out the area of a 12 inch pizza vs a 16 inch pizza before calculating the cost per square inch.  So in this exercise you've already calculated area and calculated the unit cost or cost per square inch, both real life math.

Rather than relying on the book for numbers, why not pop down to one or more pizza places, pick up menus with prices and use those.  Students can compare establishments to see who has the best buy for the price.  The comparisons should include places like Papa Murphy's which lets you bake the pizza and some of the ones only in your town.  It is important to look at pizza's that are the same.

Furthermore, you can have students compare the area of one large pizza with the area of two small pizzas to see which situation is the best purchase.  If you have one 16 inch pizza vs two 8 inch pizza's, one might assume they are the same but if you do the math 2 * 8^2 * 3.1415 you'd get 402.11 square inches vs 16^2*3.1415 or 804.22 square inches.  So it would take four eight inch pizzas to equal the are of one 16 inch pizza.

There is also math involved in the slice itself due to Gauss's theory telling us how to calculate the object's curve.  In other words, a flat surface can be curved one direction or the other but it must retain flatness which is why its hard to gift wrap a volleyball because the paper is unable to retain any flatness.  He calculated the curve of a cylinder is zero meaning a piece of paper could be folded into a cylinder while the curve of a volleyball is nonzero because you cannot fold the paper into a sphere.

If you hold the pizza in your hand to eat, it is flat side to side and droops while you eat it because the "line of flatness" runs horizontally or across the pizza but  if you fold it in the middle so the side meet in the middle, it becomes stiffer and easier to eat because the "line of flatness" runs vertically or from the edge to the middle.

This article goes even further to break down the cost of making a pizza from scratch. The author wrote the article in July 2018 and shopped at War-mart.  Everything thing is broken down to exact amounts needed.  The author calculated it would take $.22 cents for the 11 ounces of flour needed for the pizza dough.  The yeast cost $0.44 based on buying three packets of yeast but the cost might be cheaper if she'd bought a bottle of yeast.  Total cost of the dough ran to $.88 cents for two 12 inch pizza's.

The sauce, cheese, and sausage ran a total of $1.72 for one pizza or $3.44 for two pizzas.  The author even discusses the cost of electricity which varies from location to location.  I've lived in places where it runs $.34 per KWH which is much higher than most.  The bottom line is a 12 inch pizza cost the person $2.36 to make at home rather than $16.00 at the pizza parlor.  If you do not have a grocery store near you, calculations could be done using prices off of Amazon.

According to a Forbes article from 2017, pizza both standard and upscale version have the highest markup of any food served by restaurants.  They even break down the cost of a meat pizza vs a Margarita (tomato, mozzarella, and basil) pizza.  This gives students a perspective on mark-up.

Three ways to look at pizza mathematically and none involve fractions.  Let me know what you think, I'd love to hear.  Have a great day.

Warm-up

If a plain cheese pizza costs $0.89 to make and sells for $8.00, what is the percent mark-up?

Warm-up

If it costs $1.90 to make a cheese and meat pizza, and it is sold for $14.00, how much is the mark-up?

Wildfires and Math.

There are certain places in the United States where forest fires occur regularly.  California is one while Alaska is another.  There are enough fires burning around Fairbanks that the air is extremely smokey from the ground to the sky.

Stores are selling out of masks, air purifiers, and furnace filters.  I bet you wonder about furnace filters.  You put one in the window between the window and the box fan so as it draws air in, it is filtered and healthier.

There are costs and mathematics involved in a forest fire can be both obvious and hidden.  Obvious costs include the number of firefighters, firefighting equipment, lost houses, and lost forests but the not so obvious ones include increased illness, increased sales of air purifiers, air masks, etc.

There was a person at Kings College in London who looked at 88,000 fires in the United States between 1970 and 2000.  They discovered the fires fit the power-law relationship in that there are way more smaller fires and the numbers of fires decrease as they get larger.  In addition as the fires are looked at from east to west, the ratio of smaller fires to larger fires decrease.  Furthermore, it has been discovered that wildfires are actually a balance between the equations of energy and fuel.  In other words, fuel loss due to being burned relates to the reaction rate of fuel.

Mathematicians have also created computer programs called fire models that allow state and federal agencies to predict how these fires will spread.  The results of these programs help officials determine where to focus their firefighters and equipment or evacuate people but these programs cannot always predict sudden changes of direction that happen when the wind direction changes or grow larger.

Computer programers and mathematicians adjusting and fine tuning these programs to include detailed satellite data, and the understanding that fires create their own weather which can cause them to spread even more.  Unfortunately, these new programs often take several days to run so the information is not always helpful so officials often resort to the older models.  On the other hand, the information from the improved programs can be used to determine what drives a wildfire thus making it easier to figure out how to provide protection to communities in the future.

It has been determined that 84 out of 100 wildfires are started by humans either on purpose or by accident.  In addition, human interference has made some fires worse by working to prevent natural fires using a technique called suppression.  This policy means there has been more wood on the ground so when a spark hits, there is more fuel for fires and they burn hotter and harder.

There is a group of scientists who are creating a new program to determine how the fires interact with the weather.  They've discovered that they can use complex math and fluid dynamics to explain how the air moves after it is heated and how the motion affects the fire.  The program is built upon the math used to forecast weather.  This aspect explains why fires can suddenly spread even though there is no naturally occurring wind.

Other scientists are looking at how firebrand or embers transfer heat when they land or how fuels burn under various conditions.  Embers burn as they fly and its density changes which in turn effects how it flies out from the fire or travels in the air.  Furthermore, the characteristics of the ember is based on whether it is from vegetation or a burning building.

Within the scientific community, they are exploring  a variety of aspects of wildfires using mathematics so state and federal agencies can use the results from all of these programs to plan their response to different situational fires.  It is important because they better they can respond to the situations, the lower the damage.

Let me know what you think, I'd love to hear.  Have a great day.

Rocketry Math

One of the stops the tour made before going to the Golden Spike National Park was to look at all sorts of rockets, motors, and parts.  The big rockets seen in the background is Space Shuttle reusable solid rocket motor while the two medium sized ones in the left front are the Trident 1 and the Minuteman I.

This is the type of unit one could coordinate with the science department by looking at the mathematics involved in launching model rockets and build and launch them.  In addition, have the Social Studies teacher add in the history of the United States Space program while the English teacher could have students read one of the numerous books on this topic.

Estes Rockets has a lovely 97 page pdf with lessons on launching rockets, finding the center of mass, finding the center of pressure, rocket stability, math and rocket flight, aerial photography, and launching payloads.  It includes the lesson plans, student worksheets, and overheads although we tend to project straight onto boards.

The lessons have all the mathematics and explanations needed to complete the unit so if you aren't sure about the equations needed, they are here.  This is also geared for grades 5 to 12.  If you work with students who are of a lower grade or their skills are not where they should be, this site has a guide for elementary grades but it explains in more detail on how to find the height of a rocket in the air, determine its speed, and acceleration and flight.

The second packet would make a good introduction since as it explains things with lots of nice diagrams and it integrates reading into the classroom.  Now if you look here, Estes Rockets also offers additional cross curricular suggestions for integrating rockets in most subjects.  This page also lists all the curriculum packets they've made.

Let's not forget NASA for information on Rocketry and math.  Many of these lesson are on things like thermal protection or how to keep your rocket from burning up.  Although this thermal protection challenge is more science, it does include information on the math being used in the unit.  This makes it easy to connect with real life applications.

The NASA lessons cover all grades from K to 12 so if you are not a high school teacher there is something for you and all the lessons include a math connection.  The thing through this all is that we are almost to the 50th anniversary of the landing of Apollo on the moon.  They didn't have the computing power available we have to day and for those early flights, they relied on human calculators to make sure the math was correct.

Let me know what you think, I'd love to hear.  Have a wonderful day.

Promontory Summit, Utah.

The other day, I got to visit the Golden Spike National Park in Promontory Summit, Utah.  This is where the two railroads met, creating a transcontinental railroad.  It is where one came from the east and the other came from the west.

The engine on the left burns 3 cords of wood every 30 miles to heat the water in the 850 gallon boiler. The one on the right burned 9 tons of coal every 120 miles to heat the water in its 850 gallon boiler.  Both engines had a 2000 gallon reserve in its back around the fuel.  Consumption is based on a speed of 25mph.

Right here some cool math with just these facts.  One can tell by the chimney's which is wood and which is coal.  The short squat chimney is built that way to keep embers from flying out and setting things on fire.

The wood burning engine came from the west while the coal burning came from the east.  Think about it this way, the Central Pacific Railroad built 734 miles of track while the Union Pacific laid 1032 miles.  So using the information in the second paragraph, it is possible to figure out how many cords of wood were used coming from the west and calculating the amount of coal used to drive all 1032 miles.

The project began in 1865 and took five years to build.  The Union Pacific built 40 miles of track the first year, 260 the second, 240 the third year, and 500 miles the fourth year.  How many miles did they build the last year?  This website has more problems like this one.

This site offers another worksheet with additional math.  This one looks at ratios and fractions and more about the Chinese who helped build the Central Pacific Railroad.  It evens goes into the number of ties per mile.

It would be cool to teach transcontinental railroad related math in the math class when its being covered in the history class so students see things are related rather than everything existing in a vacuum.

Let me know what you think, I'd love to hear.  Have a great day.

Air travel

I've been traveling a lot this summer.  I've gone on line to my favorite airline to find the best fares that take the least amount of time although it can sometimes be hard.  I am late with this because one of my flights had a few hour wait in the airport, the airlines kept switching gates.

I've found some of the cheaper flights are ones that either go through multiple airports or have long as in 12 hour layovers between flights.   I try very hard to stay away from those and I try to aim for no more than about 5 hour layovers but I do not like anything less than 2 hour between flights.  This is simply because 20 to 40 minutes may sound great on paper but it does not mean it will work.

Airline prices are no longer as stable as they used to be.  One day, the flight may be $350 round trip while the next day it might be $450 round trip.  In addition, there may not that many airlines to choose from because over the past 20 to 30 years, many have gone out of business or merged.  So let's look at what factors control the setting of prices at this point in time.

Potential travelers are divided into two different groups, leisure and business and each is priced very differently because leisure travelers can plan several months to one year in advance and are more flexible in their dates while business travelers often must find flights a day or two in advance and have little choice as to when they travel.  The decision as to whether its leisure or business is often determined by the routes and when the reservation is made.  Either way, in the end, the cost is determined by what the market will bear.

In regard to leisure passengers, the airline sets the price and adjusts according to how the market responds while for the business passengers, they set the price relatively low and raise it the closer to the departure time.  The thing is, technology is being used to create the prices rather than basing them on the over all cost of the flight including fuel and taxes.

Many airlines are beginning to set the cost of flights according to the amount of extras one gets in the flight.  For instance, some airlines offer super cheap economy fares which may offer just the seat but you pay for the location and carry on with very little more, regular economy that might include a check through, free seat selection, or possibly a meal.  Then there is business class which offers more and finally first class where you get all the amenities.

In addition, the type of plane will determine how the types of seats are distributed and how many of each type.  This means the fare is often determined by the type of class such as first class, business, economy, or super saver and the type of ticket such as refundable, weekend, etc.  Both factors effect the price.  On some days such as Tuesdays, you might find the cheapest price lower because it is not one traditionally used by most business people.  Once the cheapest fairs are gone, they are gone.

Most times, the prices are higher for last minute travel because people who must travel will pay the higher prices and it helps airlines maximize profits.  Prices can also be higher leading up to certain holidays such as July 4th, Thanksgiving, or Christmas yet the actual holidays might have a lower fair.  It's just a matter of looking.

Furthermore, there are websites one can check that use technology to look for the lowest price on a route.  I do not use those because when I travel within the state of Alaska, there really isn't much choice on who you can use and the prices can be pretty standard.

This is just a brief look at how airlines set ticket prices.  Let me know what you think, I'd love to hear.  Have a great day.

Long Division vs Synthetic Division of Polynomials.

 Most math teachers end up teaching both long division and synthetic division of polynomials at some point in the classes.  I know that most of my students never take time to ask why they need to learn both when synthetic is easier.

They do not recognize that one is only used with an expression to the first power while the other can be used with anything.  The two are related.

Long division can be used to divide one polynomial by another polynomial that is of a lesser degree.  You can use long division to divide a problem such as x^4 + 3x^3 - 2/x^3 + 4.
You don't need to rewrite anything.

Synthetic division, on the other hand, only works when you are dividing a linear term (degree one) into a higher degree polynomial.  So this one is restricted to a very limited pool of polynomials.

This is one reason why you cannot use synthetic division for every single problem unless you can easily factor the polynomial you are dividing into the other polynomial such as x^2 - 1 or x^2 +4x + 4.  These you can quickly factor those to get the degree one polynomial so you can use synthetic division.

The other problem with using synthetic division instead of long division is that it sometimes becomes much harder when you have something like 3x + 2 = 0, you have to rewrite it to x = -2/3 so you are. using fractions where as when you do the division using long division, you do not have to rewrite anything and do not have to work with fractions.

I teach both ways but I haven't always taken time to explain why you might use long division rather than synthetic division even though it is easier for people to do.  Let me know what you think, I'd love to hear.  Have a great day.  This is a bit short but I've been working at a conference and didn't have a lot of time.  I hope to get back to normal tomorrow.

Warm-up

If the redwood tree grows at a rate of 9 feet per year, how old is the tree if it is 65 feet tall.

Warm-up

If the redwood tree grows at about 9 feet per year, how tall will it be after 72 years.

Out Till Saturday

I am at a conference in Utah.  I will return to warm-ups tomorrow and regular columns on Monday.

July 4th

Numerical Facts About Independence Day Fireworks Shows

 I find it interesting to read up on facts about certain things.  Since tomorrow is July 4th and July 4th is associated with fireworks show in places throughout the United States, I thought I would take a look at facts containing mathematical facts.

To begin, we do not have fireworks shows in Fairbanks Alaska because the night sky does not get dark enough so they save the fire works for New Years when it is quite dark.

1. Macy's 4th of July celebration uses 55 times as much as the average show. This year, they are due to fire 3000 shells per minute for a 25 minute show.  It takes 60 pyrotechnic people to run the display and each shell is shot 1000 feet in the air.  In addition, there are 1600 lines of code to make sure everything happens in the proper order. The total cost of the show is $6,000,000 but it costs another $50,000 to clean up after the event.

2.  There are an average of 14,000 shows on July 4th.

3.  A short basic show can run between $2,000 and $8,000.  This is one without music, computers, or larger shells.

4. If you want computer coordination, music or larger shells, the show costs about $2,000 per minute or around $20,000 for a full show.

5. Washington, D.C. has the reputation for using the largest number of 6, 8, and 10 inch shells.  The larger the shell, the higher it goes before exploding and you can figure about 100 feet per inch as a rule of thumb so a 6 inch shell explodes at about 600 feet.  In addition, they use 33 tons of fireworks that are exploded over a 33 minute period.

6.  The larger shells can cost up to $336 each.

7.  Fireworks require permits in order to set them off but prices range from free to over $500.  Some companies include the permitting cost as part of the complete package while others charge a separate price.

8.  Fireworks permits often require the company putting on the fireworks show to have anywhere from $1,000,000 to $5,000,000 worth of insurance just in case something happens.  This means the group who does the hiring will be charged upwards of $10,000 for their insurance contribution and many locals require extra duty police to be hired. An average figure for extra duty police is $50,000 or more.

Now with all these facts, it is possible to create questions such as how many shells will Macy's use during their July 4th celebration.  Answer is 3000 x 35 = 105,000 shells.

What sized shells is Macy's using in order for the fireworks to explode at 1000 feet?  Answer 10 inch shells.

How much does it cost for shells every minute during the Macy's fireworks?  Answer $336 x 3000 =
$100,800.

The three question are examples to use data from the 8 facts.  There are more possible questions but by asking questions, it helps students read for understanding and to learn to choose the correct data.  It is real life communications.

Let me now what you think, I'd love to hear.  Have a great day.

Interest Rates Continued

 Today, I"ll discuss various types of interest and what controls them.  One of the primary influence is the prime rate but there are other factors.

For instance, historically mortgage rates were influenced by treasury rates or the rate the government pays to borrow money but more recently, its based on a secondary market that bundles and sells mortgages.  At one point, mortgage rates hit a high of over 16 percent in 1980 but it slowly came down to around 3 or 3.5 percent.

Some financial institutions pay interest on checking accounts but there are only a few who do so and the interest they pay is very little.  This interest is what the bank pays to use your money while it is in the bank.  It began around .11 percent but dropped to .04 percent.  Banks do pay interest on money held in a savings account but the interest rate is fairly low because they can borrow money from the Federal government at a discounted rate.

For a while, banks were offering higher interest rates on savings accounts because they were writing lots of mortgages and rather than let their reserves drop, they used the increased interest rates to attract more savings deposits.  Once the housing bubble broke, interest rates on savings accounts have dropped to under one percent.

In addition, the interest offered for savings accounts have to be less than the interest rate for money loaned out, otherwise they cannot make a profit.  So in general, the higher the interest rates on mortgages and personal loans, the higher the savings interest and vice versa.

If students ask why the bank needs to make a profit, you can point out that the bank has to have money to pay for the building either rented or owned, has to pay for salaries of its employees in addition to benefits, utilities such as electricity, sewer, water, heat, and taxes.  The difference on the interest between what they loan out and what comes in is also used to help keep the reserves up as required by the federal government.

So know as a teacher you know more about how interest rates are set and why they are the way they are.  Let me know what you think, I'd love to hear.  Have a great day.

What Controls Interest Rates.

 When people wish to purchase something such as a car or house, they often shop around for the best deal they can.  Sometimes it requires a higher down payment to get the better interest rate while other times, its a special designed to get rid of inventory.

Historically, interest rates have been all over the place from lows of 1% to 12 or 13%.  When discussing interest rates, there are three different ones which effect current rates.  One is the Prime rate, another is the Federal Fund rates, and the last is the Discount interest rate.

The Prime rate is actually the federal interest rate, usually tied to mortgage rates, money market accounts, and CD's or Certificate of Deposits.  This is the rate that financial institutions use to set interest rates on loans.  It is also tied to variable rate credit cards and loans so if the prime rate goes up, the interest rate associated with these vehicles also goes up.  Over the past 100 years, prime rates have gone from 1% to an all time high of 21.5% in 1980.

The Fed Fund rate is the rate banks pay to borrow money from other banks.  This happens if their minimum amount of money in reserves falls below a certain amount based on the amount of money they have from customers.  When this rate goes up, there is less money available for bank to bank loans.

Originally, in the 1920's, bank to bank loans were based on stock exchange call loans rate.  Unfortunately, when the crash of 1929 hit, the call loans stagnated so rates stayed at 1% through the depression and 1930's.  When World War II hit, rates were kept low due to the war but once the 1950's arrived that Federal Fund market set bank to bank loan rates. The rates rose to over 16% in 1981 before declining.

Finally, the Discount Interest Rate is the rate banks are charged to borrow money from the Federal Reserve for a short time.  This rate is set by the Federal Reserve banks and falls into one of three classifications - primary credit, secondary credit, and seasonal credit.  Each has its own credit rate and all loans are secured.

These are the three main influences on regular loans but there are other things that influence the interest paid on savings accounts, credit cards, etc.  Tomorrow I'll go into those.  I've taught calculating interest using simple and compound formulas but I've never known how certain rates were set.

Let me know what you think, I'd love to hear.  Have a great day.